Soft Actor-Critic:
Off-Policy Maximum Entropy Deep Reinforcement Learning
with a Stochastic Actor

An Analysis of Soft Actor-Critic

We apply reinforcement learning (RL) to robotics tasks. RL can solve sequential decision making problems through trial and error. In recent years, RL has been combined with powerful function approximators such as deep neural networks to solve complex robotics tasks with high-dimensional, continuous state and action spaces. Soft Actor-Critic (SAC) [1] is a state-of-the-art model-free RL algorithm for continuous action spaces. It adopts an off-policy actor-critic approach and uses stochastic policies. It uses the maximum entropy formulation to achieve better exploration. SAC achieves better performance than other off-policy as well as on-policy RL algorithms on standard continuous control benchmarks in simulation. Recently, the authors also successfully trained SAC on some real robots in under a few hours. Hence, the Soft Actor-Critic paper is important from both a general RL as well as robotics perspective. Hence, we decide to analyze it.

Related Work

The related work section of the paper "Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor" by Haarnoja et al. discusses several key themes in reinforcement learning literature:

  1. Actor-Critic Frameworks: The section reviews the derivation of actor-critic algorithms from policy iteration, referencing foundational works such as Barto and Sutton's "Neuronlike Adaptive Elements That Can Solve Difficult Learning Control Problems" (1983). Many actor-critic algorithms, like those discussed by Peters et al. (2008), use on-policy policy gradient formulations for actor updates, and some incorporate entropy as a regularizer, as seen in works like Schulman et al.'s "Proximal Policy Optimization Algorithms" (2017).
  2. Off-Policy Training: The challenges of on-policy training in large-scale reinforcement learning problems are discussed, and the paper references efforts to enhance sample efficiency through off-policy samples and higher-order variance reduction techniques. Lillicrap et al.'s "Continuous Control with Deep Reinforcement Learning" (2015) is mentioned as an example, highlighting challenges with its stability and sensitivity to hyperparameter settings.
  3. Maximum Entropy Reinforcement Learning: The paper introduces the concept of maximum entropy reinforcement learning, citing applications in inverse reinforcement learning (Ziebart et al., "Maximum Entropy Inverse Reinforcement Learning" - 2008) and optimal control (Todorov - 2008; Toussaint - 2009; Rawlik et al. - 2012). The idea of using maximum entropy to guide policy learning in guided policy search (Levine et al. - 2013, 2016) is also discussed.
  4. Connection between Q-learning and Policy Gradient Methods: The authors highlight recent papers that explore the connection between Q-learning and policy gradient methods in the context of maximum entropy learning. Works by O'Donoghue et al. ("The PGQ Algorithm" - 2016), Haarnoja et al. ("Reinforcement Learning with Deep Energy-Based Policies" - 2017), Nachum et al. ("Bridging the Gap Between Value and Policy Based Reinforcement Learning" - 2017), and Schulman et al. ("Equivalence Between Policy Gradients and Soft Q-Learning" - 2017) are referenced.
  5. Comparison with Prior Maximum Entropy Methods: The section notes that prior maximum entropy methods, such as those approximating the maximum entropy distribution with a Gaussian (Nachum et al. - 2017) or using a sampling network (Haarnoja et al. - 2017), generally do not outperform state-of-the-art off-policy algorithms like DDPG. The authors emphasize that their proposed Soft Actor-Critic algorithm surpasses the performance of prior off-policy methods in terms of both efficiency and final results.

In summary, the related work section provides a comprehensive overview of key concepts and references in the field of reinforcement learning, contextualizing the Soft Actor-Critic algorithm within the existing literature.

Biography

  1. Tuomas Haarnoja: PhD from Berkeley. Currently a Research Scientist at Deepmind.
  2. Aurick Zhou: Currently a PhD student at Berkeley.
  3. Pieter Abbeel: PhD from Stanford. Currently a Professor at Berkeley.
  4. Sergey Levine: PhD from Stanford. Currently a Professor at Berkeley.

Methodology

Maximum Entropy RL

In maximum entropy RL, the objective is to maximize the expected return while acting as randomly as possible. By doing so, the agent can explore better and capture different modes of optimality. This also improves robustness against environmental changes.




An agent trained using the maximum entropy RL objective explores both passages during training.

The entropy of a random variable is given by, $H(X) = \underset{x \sim P}{\mathbb{E}}[-\log P(x)] $. Thus, we define the maximum entropy RL objective as, $$ \pi^{*} = \underset{\pi}{\arg\max} \underset{\tau \sim \pi}{\mathbb{E}} \big[\sum_{t=0}^{\infty}\gamma^{t}\big(\;r(s_{t},a_{t},s_{t+1})+\alpha H(\pi(\cdot|s_{t}))\;\big)\big] $$ Here, $\alpha > 0$, is the weightage given to the entropy term in the objective. $\alpha$ is also referred to as the "temperature". We define the value function to include the entropy from every timestep, $$ V^\pi(s) = \underset{\tau \sim \pi}{\mathbb{E}}\big[\sum_{t=0}^{\infty}\gamma^{t}\big(\;r(s_{t},a_{t},s_{t+1})+\alpha H(\pi(\cdot|s_{t}))\;\big)\; \big | \;s_{0}=s\,\big] $$ We define the action-value function to include the entropy from every timestep except the first, $$ Q^\pi(s,a) = \underset{\tau \sim \pi}{\mathbb{E}}\big[\sum_{t=0}^{\infty}\gamma^{t} r(s_{t},a_{t},s_{t+1}) + \alpha \sum_{t=1}^{\infty} \gamma^{t} H(\pi(\cdot|s_{t})) \; \big | \;s_{0}=s,a_{0}=a\,\big] $$ Thus, $$ V^\pi(s) = \underset{a \sim \pi}{\mathbb{E}}[Q^\pi(s,a)] + \alpha H(\pi(\cdot|s)) $$

SAC

In SAC, we have,

  • a single policy network, $\pi_{\theta}$
  • two Q networks $Q_{w_{1}} \; , \; Q_{w_{2}}$
  • two target Q networks $Q_{w_{1}^{'}} \; , \; Q_{w_{2}^{'}}$
We train both Q-functions to regress a single shared target y, which is computed using target Q-networks and makes use of the clipped double-Q trick. $$ y = r + \gamma \; (\; \underset{i=1,2}{\min} Q_{w_{i}^{'}}(s',a') - \alpha \log \pi_{\theta}(a'|s') \;) $$ The next-state actions used in the target come from the current policy instead of the target policy. The loss function is given by, $$ L(w_{i}) = \underset{(s,a,r,s')\sim \mathcal{D}}{\mathbb{E}}[\;( Q_{w_{i}}(s,a)-y )^{2}\;] $$ In policy learning, the objective is to maximize, $$ V^\pi(s) = \underset{a \sim \pi}{\mathbb{E}}[Q^\pi(s,a)] + \alpha H(\pi(\cdot|s)) $$ The policy is stochastic, therefore actions are sampled. To be able to backpropagate through sampled actions, we use the reparameterization trick. The policy outputs the mean $\mu$ and standard deviation $\sigma$ of a Gaussian distribution. We then sample a gaussian noise $\epsilon \sim \mathcal{N}(0,\mathbb{I})$. We then combine the noise with the policy outputs and use tanh to squash the action to [-1,1]. $$ a = a_{\theta}(s,\epsilon) = \text{tanh}(\mu_{\theta}(s)+\sigma_{\theta}(s)\cdot \epsilon) $$ We rewrite the expectation over actions in the objective into an expectation over noise, $$ \underset{a\sim \pi_{\theta}}{\mathbb{E}}[\; Q^{\pi_{\theta}}(s,a) - \alpha \log \pi_{\theta}(a|s) \;] = \underset{\epsilon \sim\mathcal{N}}{\mathbb{E}}[\; Q^{\pi_{\theta}}(s,a_{\theta}(s,\epsilon)) - \alpha \log \pi_{\theta}(a_{\theta}(s,\epsilon)|s) \;] $$ Thus, the objective becomes, $$ \underset{\theta}{\max} \underset{\epsilon \sim\mathcal{N}}{\underset{s\sim \mathcal{D}}{\mathbb{E}}} [\; (\; \underset{i=1,2}{\min} Q_{w_{i}}(s,a_{\theta}(s,\epsilon)) - \alpha \log \pi_{\theta}(a_{\theta}(s,\epsilon)|s) \;] $$

Algorithm

Here, the temperature $\alpha$ is a hyperparameter.

Implementation

You can find my Pytorch implementation of SAC for continuous action spaces at https://github.com/adi3e08/SAC.

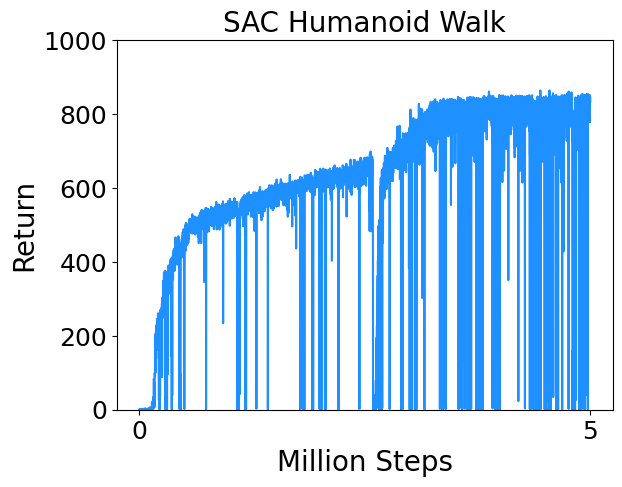
Results

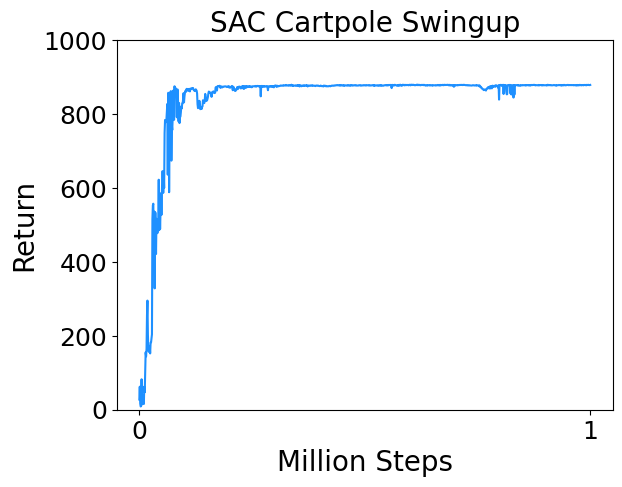
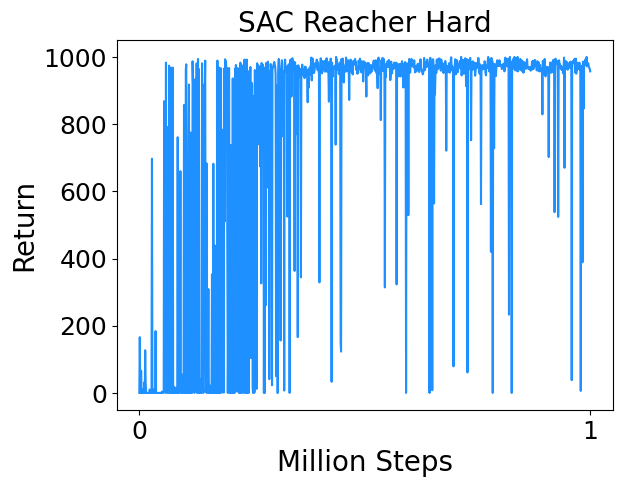
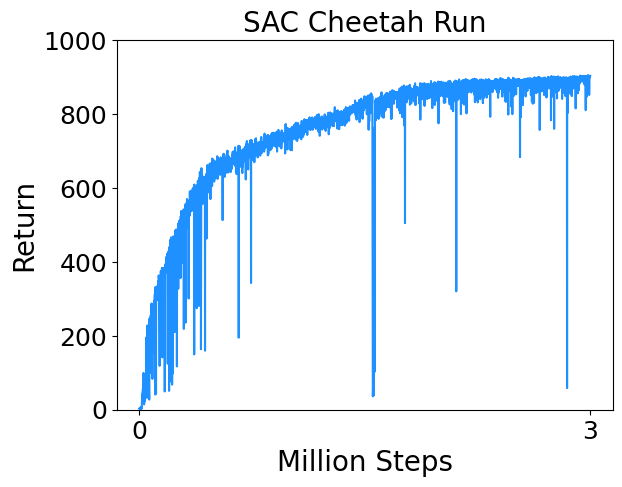
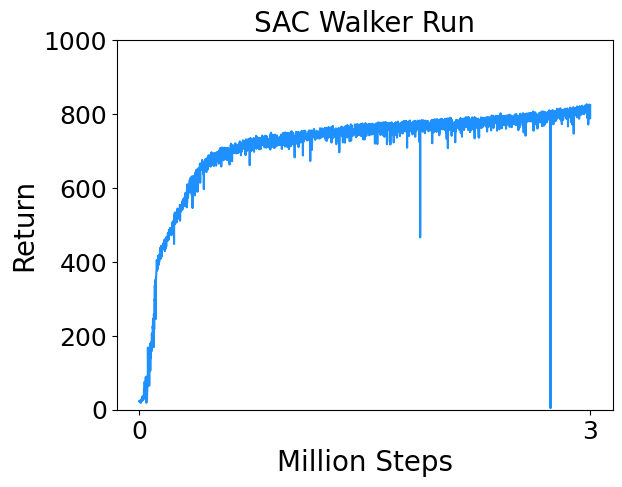
I trained SAC on a few continuous control tasks from Deepmind Control Suite. Results are below.

* Cartpole Swingup : Swing up and balance an unactuated pole by applying forces to a cart at its base.

* Reacher Hard : Control a two-link robotic arm to reach a random target location.

* Cheetah Run : Control a planar biped to run.

* Walker Run : Control a planar biped to run.

* Humanoid Walk : Control a simplified humanoid to walk.

Industry Applications

The Soft Actor-Critic algorithm has been successfully applied to some real world robotics tasks, such as autonomous navigation, robotic manipulation, legged locomotion etc. The off-policy formulation and scalability of the algorithm make it particularly attractive for real-world applications.

Social Impact

The Soft Actor-Critic paper's contributions to off-policy reinforcement learning, stability, and efficiency improvements have had positive implications for fields such as reinforcement learning and robotics, which in turn have had positive implications for society.

Follow-on Research

In this version of SAC, the temperature $\alpha$ is a hyperparameter. However it was found that the algorithm is brittle to the choice of $\alpha$. In follow up work (Soft Actor-Critic Algorithms and Applications [2]), the temperature $\alpha$ is learnt by minimizing the loss, $$ L(\alpha) = \alpha \; (-\log\pi(a|s)-\widetilde{H}) $$ where $\widetilde{H}$ is the entropy target. Typically, $\widetilde{H}$ is set to be equal to the negative of the action space dimension i. e. $\widetilde{H} = - \; \text{dim}(\mathcal{A})$.

Given that the Soft Actor-Critic paper introduces a novel algorithm, there could be several other directions for follow-on research. Researchers may explore further improvements to the algorithm, extensions to different problem domains, or adaptations for specific applications. Additionally, efforts may focus on understanding the algorithm's limitations and addressing challenges that arise in specific scenarios.

Peer Review

Title: Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor

  • Score: 8/10
  • Strengths: The paper introduces a novel algorithm, Soft Actor-Critic, that combines off-policy actor-critic training with a stochastic actor, addressing challenges faced by previous methods. The empirical results demonstrate superior performance in terms of both efficiency and final performance compared to state-of-the-art off-policy deep reinforcement learning methods.
  • Concerns: While the paper provides a comprehensive overview of related works, further discussion on the limitations and potential challenges of the proposed algorithm could enhance the clarity for readers. Also, the math was a little hard to follow. The authors could have simplified the math and presented it a little better.
  • Suggestions: Consider providing more insights into the algorithm's behavior in specific scenarios or environments to give practitioners a better understanding of its strengths and limitations, including comparisons with a wider range of baseline algorithms could strengthen the paper's contributions.
  • Overall Assessment:The Soft Actor-Critic paper presents a significant contribution to the field of reinforcement learning, offering a promising solution to challenges faced by existing off-policy methods. The empirical results support the claims, and the clarity of the overall presentation makes it accessible to a broad audience. Addressing minor concerns and expanding on certain points would further strengthen the paper.

References

[1] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In International conference on machine learning, pages 1861–1870. PMLR, 2018a.

[2] Tuomas Haarnoja*, Aurick Zhou*, Kristian Hartikainen*, George Tucker, Sehoon Ha, Jie Tan, Vikash Kumar, Henry Zhu, Abhishek Gupta, Pieter Abbeel, Sergey Levine. Soft Actor-Critic Algorithms and Applications. arXiv preprint, 2018.

Team Members

Adithya Ramesh.